2.6 Indexing

Indexing provides access to elements of a composite or indexable collection value. The indices are provided in a comma-separated list delimited by brackets situated as a postfix operator on an expression (see Figure 2.24). The expression being indexed is called an indicand. An alternative syntax simplifies indexing for composites. Sets, although collections, are not indexable because indexing can only be applied to an expression whose items are ordered. A double index applied to a matrix evaluates to an element of the matrix. A singleton index applied to a matrix evaluates to a tuple representing a row of the matrix.

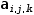
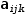
Indices can be applied as a list but they can also be applied one at a time by separating the list into singleton indexes. Note the difference between aʈ[i, j, k] (entered as aʈ[i,j,k]) and aʈ[i][j][k] (entered as aʈ[i][j][k]). Selection can be applied to the latter at differing levels of granularity.

Although indexes can be applied to value expressions, they are most commonly applied to variables. Because of Myron's late binding semantics, the value of an indexed variable is not known until evaluation time. This means that indexes cannot be strongly typed. The result is that an index can be applied to almost any type of indicand expression and also means that some index expressions cannot be evaluated.

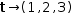
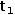
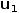
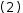
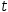
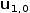
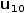
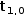
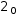
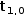
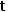
For example, consider the tuple of scalars tʈ→(1, 2, 3) and the tuple of tuples uʈ→((, 1), (, 2), (, 3)). The expression tʈ[1] evaluates to 2 and uʈ[1] evaluates to (, 2). The latter can be indexed one more time but what must happen if t is indexed twice as well? The expression uʈ[1, 0] (or the more granular uʈ[1][0]) evaluates to 2, but the same index on tʈ[1, 0] evaluates to 2[0]. This shows that indexes are applied until the indices are exhausted or the indexed expression is not indexable. Also, because of late binding the evaluation of tʈ[1, 0] depends on the definition of tʈ currently present in the workspace.

2.6.1 Indexing generators

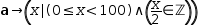
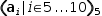
A generator or a variable bound to a generator is indexed by acquiring the index^th item in the domain sequence and then evaluating the template, as bound to that item. For example, (x|(0≤x<10)∧(x÷2∈ℤ))[2], containing no unbound references, can be simplified; and doing so produces a result of 4. As mentioned above, complicated expressions like this are seldom indexed directly but rather assigned to a variable, which is indexed in another expression. Although the latter cannot be simplified, it can be bound and evaluated. aʈ→(x|(0≤x<100)∧(x÷2∈ℤ)) is an example of a generator variable and (aʈ[i]|i∈5, 10)[5] is an example of its use in another generator, which is then indexed.

2.6.2 Indexing composite values

Complex, radial and vector variables and values can be indexed. Index 0 on complex values produces the real part and index 1 produces the imaginary part. Vectors are indexed such that index 0 produces the first, or x, component. Radials differ in that the magnitude, although the first component of a radial value, cannot be accessed by index 0. That index extracts the first angle, while index 1 extracts the second angle and so on. The magnitude of a radial is accessed by magnitude notation: 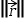|rɽ|.

2.6.3 Alternate indexing for composites

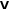
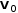
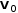
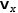
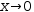
Vector. The x component of a vector vʋ is indexed by vʋ[0]. Many math textbooks use an alternate notation that exchanges the positions of the indicand and the index. That is, indicandʋ[index] becomes index[indicandʋ]. Using the alternate notation, x[vʋ] means the same as vʋ[0] (or vʋ[x] with x→0). The alternate notation applies only if the left operand is a named vector component – one of x, y or z – and the right operand is a vector. To ease the task of input, the right operand need not be typed as a vector. That is, for an expression in which the left operand is a vector component and the right operand is entered as a real variable, the right operand is rewritten as a vector variable. Thus the simplified input of the expression above is x[v].

Complex. Using the techniques for vectors, the components of a complex number can be extracted using named complex components r and i. As with vectors, if the right operand is a real variable, it is rewritten as a complex variable.

Radial. Again following the technique for vectors, the angles of a radial value (or a real variable rewritten as a radial variable) can be extracted using named radial angles θ and φ. Further angles for higher dimensional radials must be extracted using regular indexing. The magnitude can be extracted using the magnitude operator.

In summary, the indicand in an expression of the form 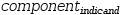component[indicand] is promoted to a type determined by the component as shown in Figure 2.34.

Component	Indicand
x, y, z	vector
i, r	complex
θ, φ	radial

Figure 2.34 Indicand promotions